동적프로그래밍을 배울 때 가장 기본적으로 이해하기 좋은 피보나치 수열에 대해 알아보자
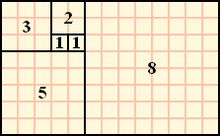
피보나치 수열
첫째 및 둘째 항이 1이며 그 뒤의 모든 항은 바로 앞 두 항의 합인 수열
1 : 1
2 : 1
3 : 2
4 : 3
5 : 5
6 : 8
.
.
.
n : n - 1 + n - 2
DP를 적용하지 않은 코드
import java.util.*;
public class Main
{
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
System.out.println(fibonacci(n));
}
static int fibonacci(int n){
if(n == 1 || n == 2){
return 1;
}
else{
return fibonacci(n-1) + fibonacci(n-2);
}
}
}
코드 설명
n = 1
1. fibonacci(1) = 1
n = 2
1. fibonacci(2) = 1
n = 3
1. fibonacci(3) = fibonacci(2) + fibonacci(1)
2, fiboancci(2) = 1
3. fibonacci(1) = 1
n = 4
1. fibonacci(4) = fibonacci(3) + fibonacci(2)
2. fibonacci(3) = fibonacci(2) + fibonacci(1)
3. fibonacci(2) = 1
4. fibonacci(2) = 1
5. fibonacci(1) = 1
n = 5
1. fibonacci(5) = fibonacci(4) + fibonacci(3)
2. fibonacci(4) = fibonacci(3) + fibonacci(2)
3. fibonacci(3) = fibonacci(2) + fibonacci(1)
4. fibonacci(3) = fibonacci(2) + fibonacci(1)
5. fibonacci(2) = 1
6. fibonacci(2) = 1
7. fibonacci(2) = 1
8. fibonacci(1) = 1
5. fibonacci(1) = 1
n이 커질 수록 중복된 연산이 매우 많은 것을 알 수 있다
이럴 때 DP를 적용하여 중복된 연산을 하지 않을 수 있다
즉 이전에 계산한 값을 기억해서 중복된 값을 계산하지 않기
배열을 이용하여 dp[n]에 fibonacci(n)의 값을 저장하면 중복계산을 하지않을 수 있음
DP를 적용한 코드
import java.util.*;
public class Main
{
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] dp = new int[1001];
dp[0] = dp[1] = 1;
System.out.println(fibonacciDP(dp, n));
}
static int fibonacciDP(int[] dp, int n){
if(dp[n] != 0){
return dp[n];
}
else{
if(n==1 || n==2){
dp[n] = 1;
}else{
dp[n] = fibonacciDP(dp, n-1) + fibonacciDP(dp, n-2);
}
return dp[n];
}
}
}
입력 n이 1000 미만인 경우라고 가정
초기 상태 :

n = 1
dp[1] = 1, return 1
n = 2
dp[2] = 1 할당, return 1

n = 3
dp[3] = fibonacciDP(2) + fibonacciDP(1) 이므로
dp[3] = 1 + 1 = 2

n = 4
dp[4] = fibonacciDP(3) + fibonacciDP(2) 이므로
dp[4] = 2 + 1 = 3

n = 5
dp[5] = fibonacciDP(4) + fibonacciDP(3)이므로
dp[5] = 3 + 2 = 5
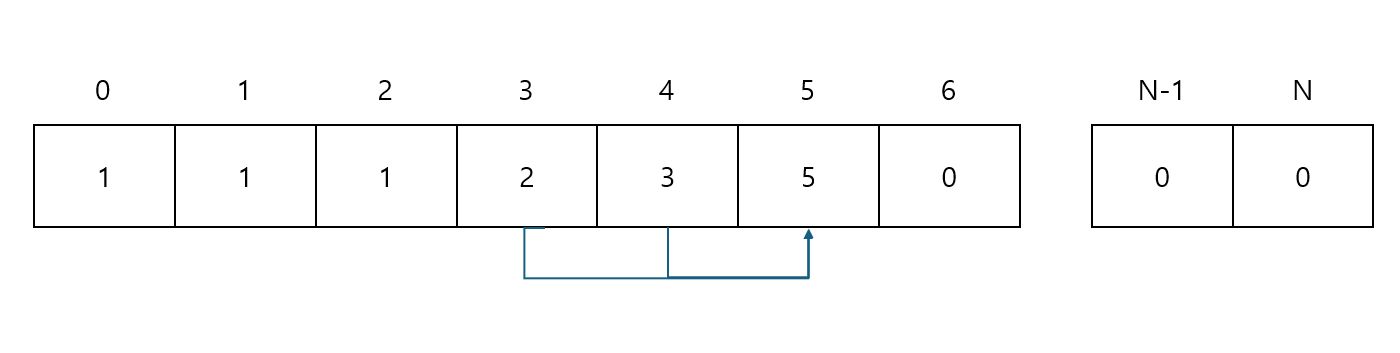
배열 그림을 보면 알 수 있듯이 이미 계산한 값들은 배열로 저장되어 있어 중복으로 계산을 하지 않아도 된다.
따라서 시간복잡도가 최악인 O(2^n)에서 O(n)으로 기하급수적으로 줄은것을 볼 수 있다.
동적프로그래밍
결국 동적 프로그래밍이란 중복되는 계산을 줄여 시간 복잡도를 개선해나가는 방법이다.
동적 프로그래밍이 어려운 이유는 스택, 큐 처럼 정형화된 자료구조가 아닌 그냥 하나의 시간 복잡도를 개선하는 기법이라 수많은 다른 코드들이 존재하기 때문이다.
따라서 DP문제를 잘 풀기 위해선 다양한 문제들을 다양한 방법으로 풀어보고, 사고력을 키우는 게 최선의 방법이다.
'Algorithm' 카테고리의 다른 글
| [코딩테스트] - 코딩테스트 풀 때 알면 좋은 함수(JAVA) (1) | 2024.05.17 |
|---|---|
| [알고리즘] - 에라토스테네스의 체 in JAVA (2) | 2024.05.15 |
| [자바]- length, length(), size() 구별하기 (3) | 2024.05.04 |
